3.4 KiB
3.4 KiB
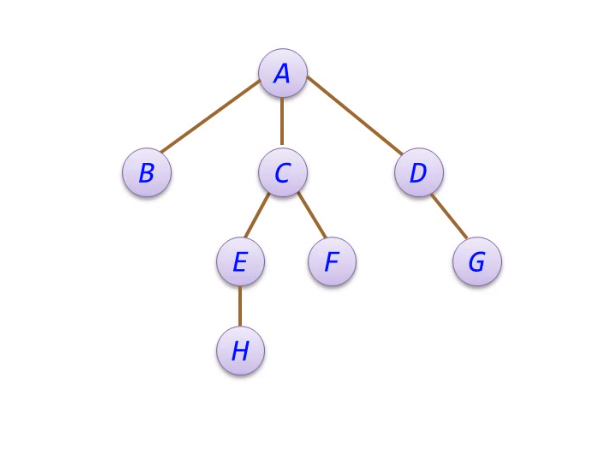
- 树是由n个节点构成的有限集合
- 如果n=0，是一颗空树
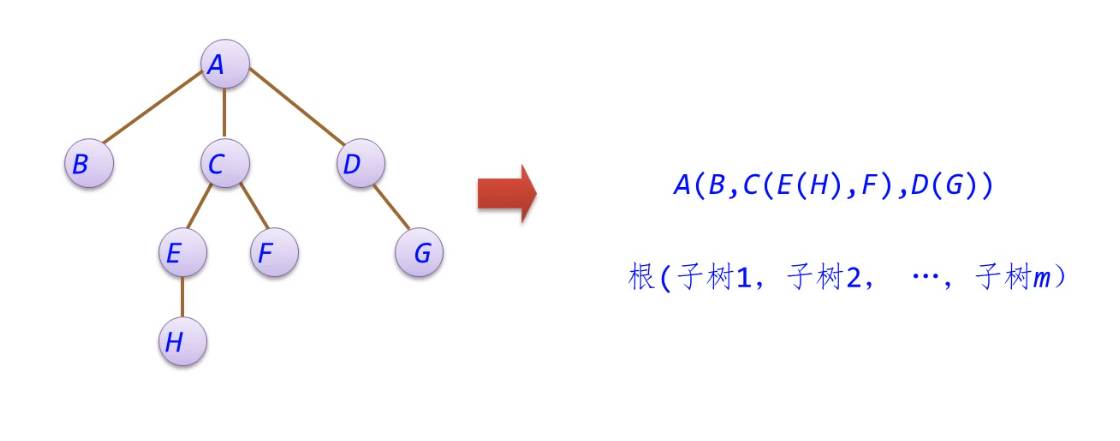
- n>0，这n个节点中存在一个节点作为根节点，其余节点可分为m个互不相交的有限集，其中每个子集本身又是一颗符合本定义的树，称为根节点的子树
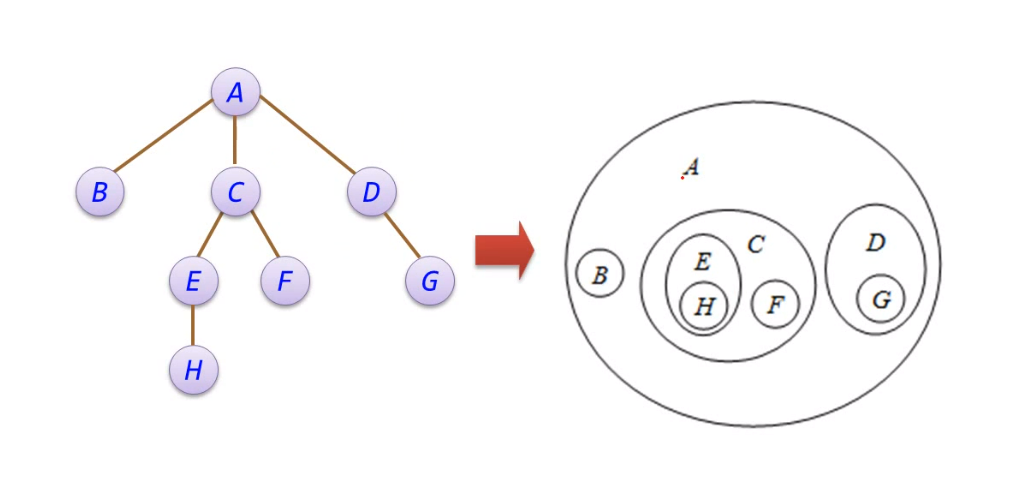
- 树是一种非线性数据结构，具有以下特点：
- 每一节点可以由零个或多个后续节点，但有且只有一个前驱节点（根节点除外）
- 数据节点按分支关系组织起来，清晰地反映了数据元素之间的层次关系
- 树的逻辑结构
- 树形表示法
- 文氏图表示法
- 凹入表示法
- 括号表示法
- 基本术语
- 度：每个节点具有的子树或者后继节点数
- 分支节点：度大于0的节点称为分支节点或非终端节点，度为1的节点称为单分支节点，度为2的节点称为双分支节点
- 树的度：数中所有节点的度的最大值称之为树的度
- 叶子节点/终端节点：度为0的节点
- 孩子节点：一个节点的后继者称为孩子节点
- 双亲节点/父亲节点：一个节点称为其后继节点的双亲节点
- 子孙节点：一个节点的子树中除该节点外的所有节点
- 祖先节点：从树根节点到达某个节点路径上通过的所有节点
- 兄弟节点：具有同一双亲的节点
- 节点层次：树具有一种层次结构，根节点为第一层，其孩子节点为第二层
- 树的高度：树种节点的最大层次称为树的高度或深度
- 森林：零颗或多颗互不相交的树的集合
- 性质
- 树中的节点树等于所有节点的度数之和加1
- 度为m的树中第i层上至多有$$m^{i-1}$$个节点，这里应该有i>=1
- 高度为h的m次树至多有$$ \frac{m^{h}-1}{m-1}$$个节点
- 具有n个节点的m次树的最小高度为
log_m(n(m-1)+1)
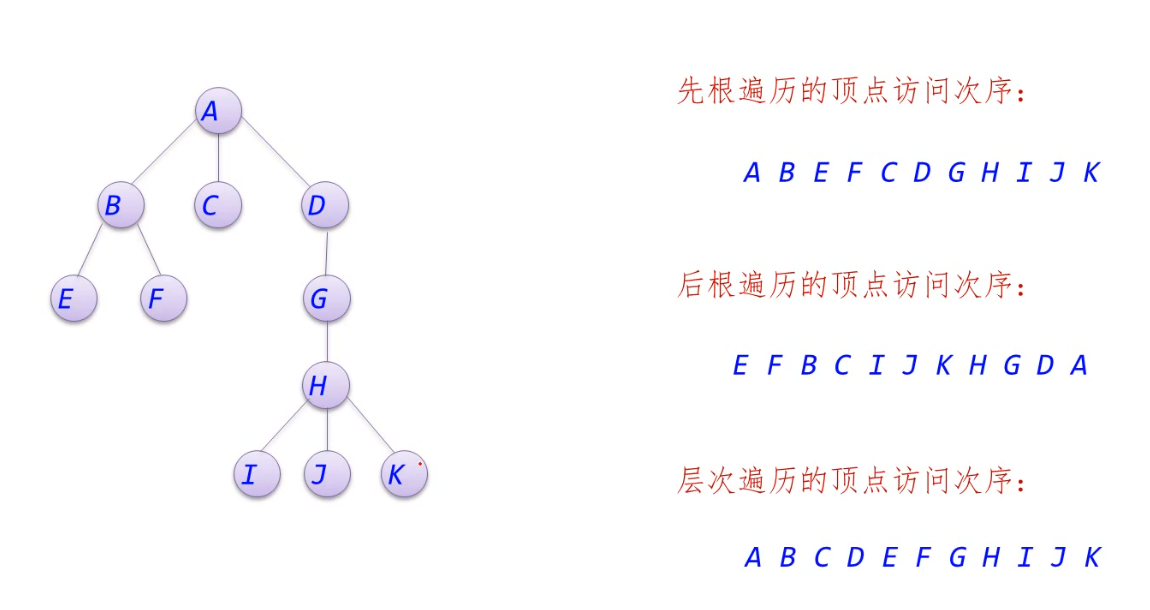
- 基本运算
- 存储结构
- 双亲存储结构
- 顺序存储结构，用一组连续空间存储树的所有节点，同时再每个节点中附设一个伪指针指示器双亲节点的位置
- 利用了每个节点只有唯一双亲的性质
- 求双亲节点十分容易，求孩子节点时要遍历
- 孩子链存储结构
- 可按树的度设计节点的孩子节点指针域个数
- 找孩子节点方便，找父节点比较困难
- 当树的度比较大时，存在较多的空指针域
- 孩子兄弟链存储结构
- 每个节点设计三个域，一个数据元素域，一个指向该节点第一个孩子节点的指针域，一个指向该节点的下一个兄弟节点指针域
- 可以方便的实现树和二叉树的互相转换
- 找双亲节点比较麻烦
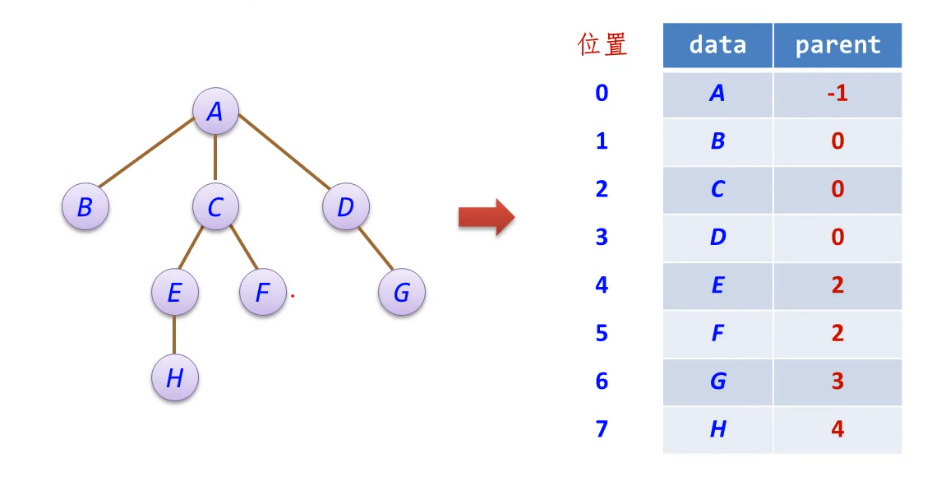
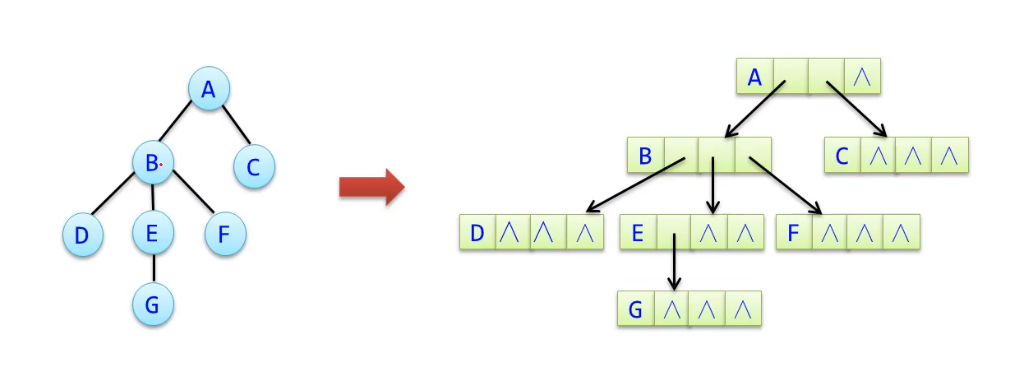
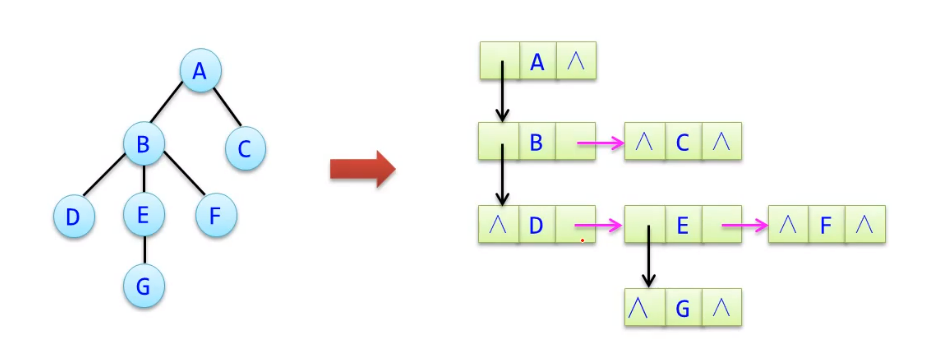
- 双亲存储结构
