10 KiB
+++ date = '2023-11-14T18:26:03.09Z' draft = false title = '187-2023.06.20.思考的真相.12' +++
在因果分析之中呢,时间这个被我们人类整个文明忽视了几千年的因素。 其实呢一直在暗中发挥着神奇甚至神秘的作用。 已经被发现呢,我们才意识到在过往的时间里,我们的思考有多么的狭隘。 。
他不夸张的讲,可能在中文世界里提及因果分析当中时间要素的重要性。 在啊科普或者是说面向民众的书籍当中课程当中,李笑来很可能都是第一人,你就明白是。
科学家们的伟大之出之后呢,在程序的菜单中找到什么呢? 叫你在文件菜单就是file那个菜单下呢,能够找到models library就是模型库? 或者你干脆按个快捷键哈,你在windows上按conttrol m或者在上去这个呃按com加上M就会跳出一个对话框,然后呢在这个对话框的呃左下角的搜索框里输入什么呢? 输入VANTV。 然后在对话框的右侧列表当中选择simple modelselcomputer science V。
科学家们的伟大之处在于说,他们中的一部分人在完成了复杂且艰辛的研究工作之后呢,还会去做科普,及用通俗易懂的方式向大众普及研究成果。 复杂性科学的核心倒也很容易说清楚。 就是什么呢? 那就是极为简单的要素和规则,经过大量的迭代,就可能涌现出原本不可想象的复杂结果。 我再重说一遍哈,就是极为简单的要素和规则,经过大量的迭代,就可能涌现出原本不可想象的复杂结果。
请注意这里几个关键词啊,简单迭代涌现,不可想象复杂。 在我们继续之前呢,我需要你在电脑上安装一个软件。 这个软件呢叫nett logo。 这是一个代理人及整合开发环境啊,但这个词是什么意思? 你先别管了,你就下载它就可以了。 你千万别担心哈,也别害怕,我不是想让你写代码啊,只不过是因为我要讲的例子啊,是需要你哈点点鼠标而已,呀,运行一个程序观察一下执行结果。 你只要有手指有眼睛有脑子就可以了。 对呀,别担心别害怕。
https://ccl.northwestern.edu/netlogo/download.shtml
NetLogo,Agent-based Programming IDE
请你放心哈,这个下载和安装是不需要专业知识的啊,以下呢是耐logo第一次运行时的画面看起来非常的简陋。 然后呢呃这个网站上呢它有logo的windows版,也有mac版啊,甚至有linux版,所以呢你安装你的操作系统相应的版本就可以了。
然后呢,打开程序之后呢,在程序的菜单中找到什么呢? 叫你在文件菜单就是file那个菜单下呢,能够找到models library就是模型库,? 或者你干脆按个快捷键哈,你在windows上按cttrol或者在上去这个呃按com加上M就会跳出一个对话框,然后呢在这个对话框的啊左下角的搜索框里输入什么呢? 输入VNT v。 然后在对话框的右侧列表当中选择simple modelscomputer science然后呢点击啊对话框右下角的open按钮,就是你打开了这个模型。
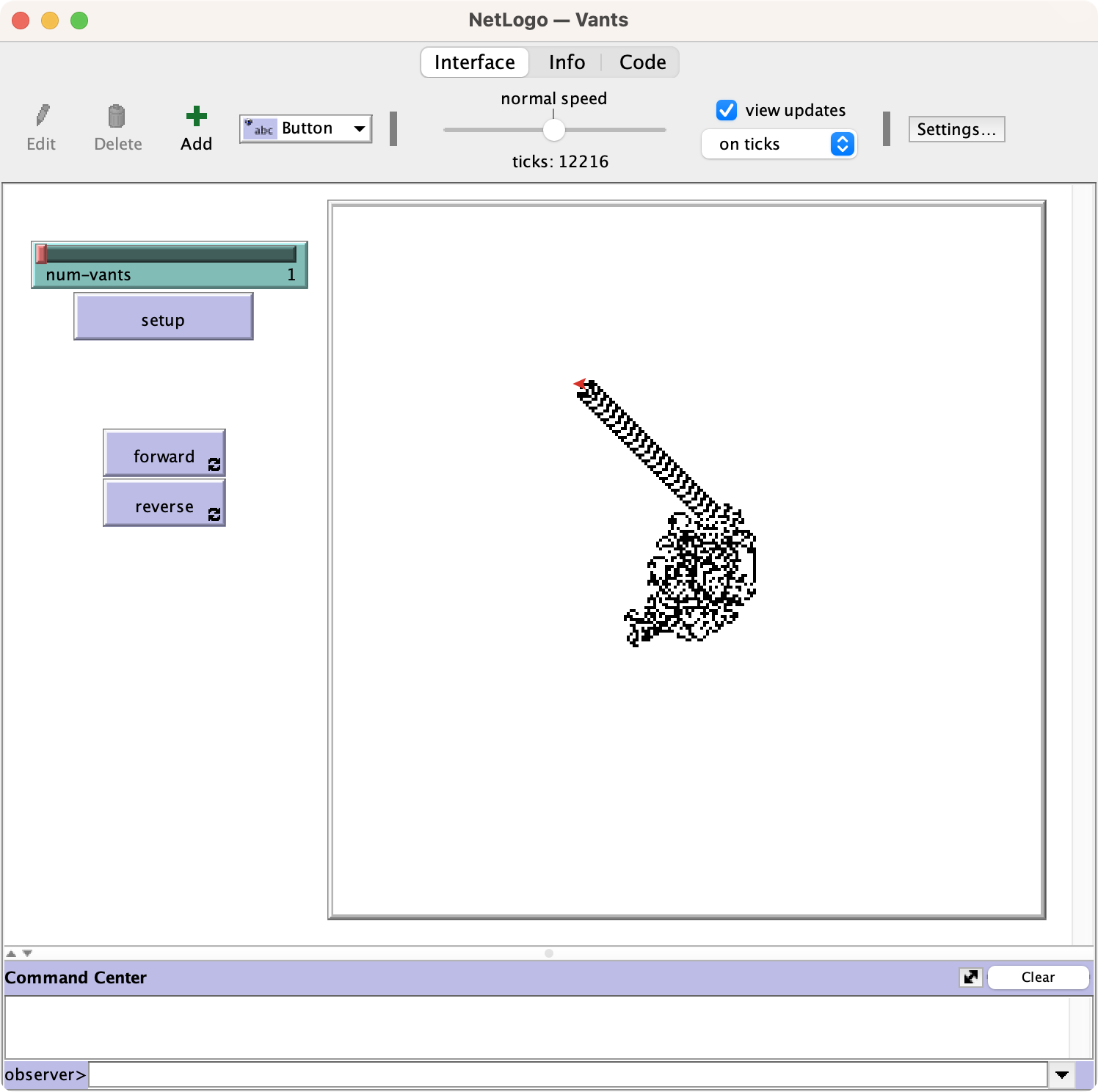
打开这个模型之后呢呃程序窗口里呢有几个按钮,然后呢,右侧的窗口里呢有一个红色的箭头,那个红色的箭头代表的是蚂蚁。 然后你需要做的是什么呢? 就是在这个VI模型被打开之后呢,先点击一下那个set up按钮,就点击一下,然后呢再点击一下forward按钮,你看看会发生什么? 嗯另外呢这个程序界面上册哈,有个滑块可以让你在程序执行过程当中随时调整执行步骤的更新。
蓝盾蚂蚁 Langton’s Ant https://en.wikipedia.org/?curid=105016
这个模型呢全称呢叫蓝登蚂蚁或者蓝顿蚂蚁呃,我这里呢给了大家哈他的 Wikipedia上的链接,它呢也是一个通用图灵机。 你看这个词你可能就听不懂了,没有关系,它是由克里斯兰顿啊,与1986年创建的。 要直到哈十几年后就是2000年的时候才被证明为图灵完整,你看什么叫图灵完整,你可能又不理解了,不过没有关系,不是关键,我们接着听下去。
但是这样的,在一个无限大的平面棋盘当中。 嗯,当然了,我们在那logo里看到的是1个50乘50啊。
这两条规则分别是什么呢? 如果这只蚂蚁呢在白色的格子里的话,那就将格子变成黑色,而后右转向前行进一步,直到什么呢? 直到下一条规则出现。 如果他在黑色的格子里的话,就将格子变成白色,而后左转前行一步,规则呢就这么简单,就这么两两两条对,而后会发生什么呢? 接下来的注意啊,接下来的发展可以被分为三个阶段。 。
- 简单
第一个阶段呢就是简单,就是在最初的几百步里呢,这是蚂蚁的足迹会不断留下非常简单的对称图形。
- 混沌
到了第二个阶段,就是几百步之后呢,它逐渐形成的是毫无规则可言的随机图形混沌。
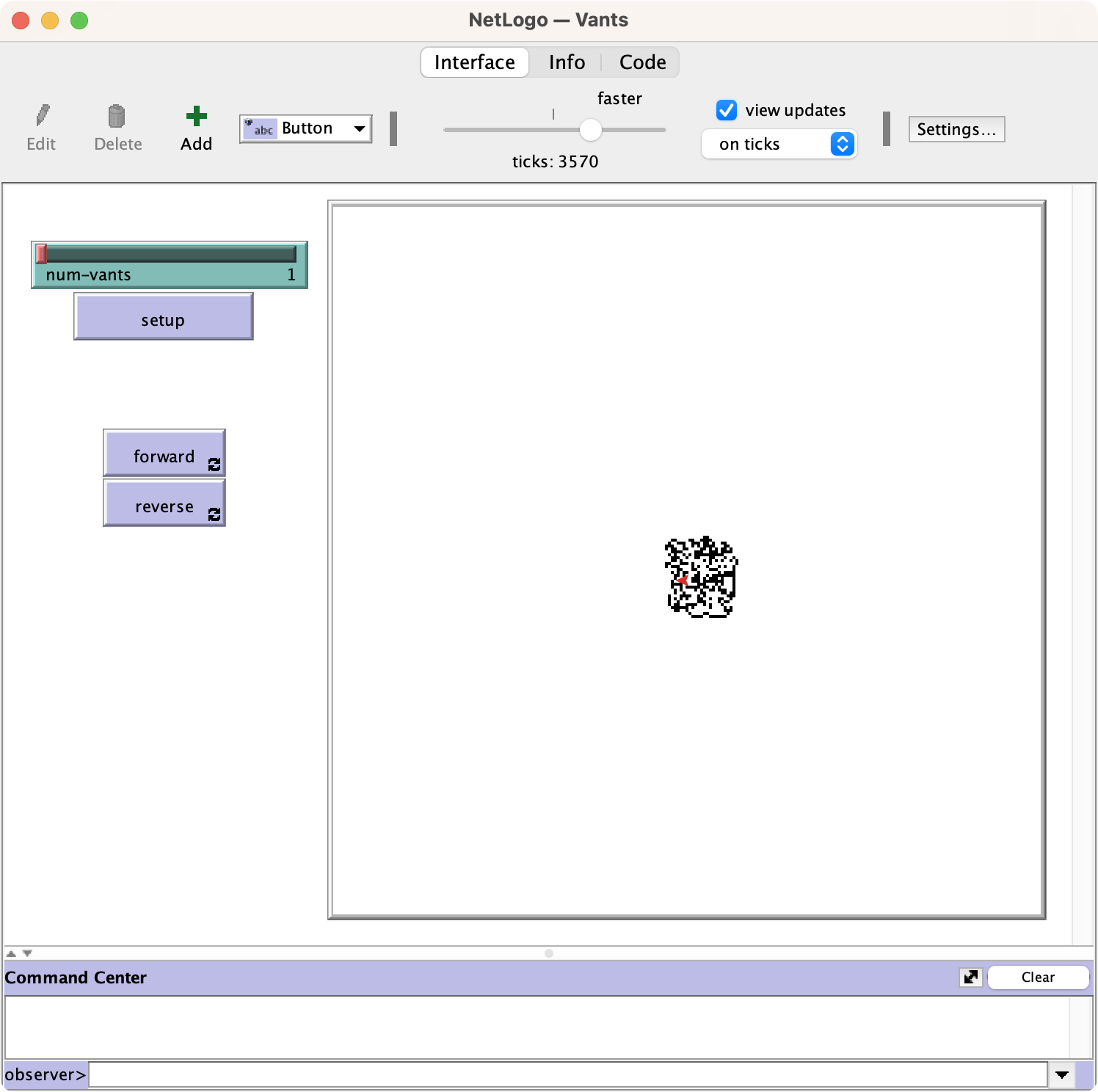
- 秩序
然后到了第三个阶段呢,叫做秩序,就是大约在一万步以后1万步啊,一万步以后秩序呢突然涌现。 这只蚂蚁呢会重复一个由104步构成的图形啊,被戏称为高速公路啊,然后呢永不停歇朝着一个方向发展。
你运行过一次之后呢,重新点一下set up按钮,你就可以恢复到起始状态。 而后呢可以重新开始让它再发展。 你会发现说每一次那个高速公路的方向都可能不一样,但无论如何,那只蚂蚁都会最终朝着一个方向驰骋。 虽然每时每刻它都好像是在绕圈子而已。 。
你盯着他的执行步骤,可以回顾一下刚才的那几个关键字,简单迭代涌现,不可想象复杂。 而后呢,再在反复执行这个模型的过程里,反复体会这几个关键字的意味。
我们可以说,因为那两个简单的规则,所以呢经过足够长的时间之后,就是重复嘛迭代嘛,那只蚂蚁终于找到了自己的方向。 但这里的关键在于说,谁都无法从一开始就能够精准预测,这样长时间的那么多次的迭代之后,涌现出来的结果。 。
这就好像谁都无法提前想象地球上的生命,从那么简单的单细胞动物开始,仅靠分裂复制变异这三个规则。 在随后的几十亿年间陆续涌现出那么丰富且那么千奇百怪的物种。 好,我们下节课再见。